Detailed Analysis of Semantic Segmentation of Diabetic Retinopathy Lesions
Received: 19-Jul-2020 Accepted Date: Aug 14, 2020 ; Published: 21-Aug-2020
Citation: Furtado P (2020). Detailed Analysis of Semantic Segmentation of Diabetic Retinopathy Lesions. EJBI. 16(3): 44-55 DOI: 10.24105/ejbi.2020.16.3.44-55
This open-access article is distributed under the terms of the Creative Commons Attribution Non-Commercial License (CC BY-NC) (http://creativecommons.org/licenses/by-nc/4.0/), which permits reuse, distribution and reproduction of the article, provided that the original work is properly cited and the reuse is restricted to noncommercial purposes. For commercial reuse, contact submissions@ejbi.org
Abstract
Diabetic retinopathy is a diabetes complication that affects the eyes, caused by damage to the blood vessels of the light-sensitive tissue of the retina. At the onset, diabetic retinopathy may cause no symptoms or only mild vision problems, but eventually it can cause blindness. Totally automated segmentation of Eye Fundus Images (EFI) is a necessary step for accurate and early quantification of lesions, useful in the future for better automated diagnosis of degree of diabetic retinopathy and damage caused by the disease. Deep Learning segmentation networks are the state-of-the-art, but quality, limitations and comparison of architectures of segmentation networks is necessary. We build off-theshelf deep learning architectures and evaluate them on a publicly available dataset, to conclude the strengths and limitations of the approaches and to compare architectures. Results show that the segmentation networks score high on important metrics, such as 87.5% weighted IoU on FCN. We also show that network architecture is very important, with DeepLabV3 and FCN outperforming other networks tested by more than 30 pp. We also show that DeepLabV3 outperforms prior related work using deep learning to detect lesions. Finally, we identify and investigate the problem of very low IoU and precision scores, such as 17% IoU of microaneurisms in DeepLabV3, concluding it is due to a large number of false positives. This leads us to discuss the challenges that lie ahead to improve the limitations that we identified
Keywords
Semantic segmentation, Diabetic Retinopathy, EFI, Deep Convolution Neural Networks
Introduction
Data Lesions that are characteristic of Diabetic Retinopathy (DR) in different stages include micro-aneurisms (MA), which are small red and rounded regions resulting from augmented capillaries, hard and soft exudates (EX, hard=HE, soft=SE), which are yellowish deposits of lipids and proteins, and hemorrhages (HA), larger blood stains that are a serious signal of advancing conditions. Proliferative Diabetic Retinopathy also exhibits neovascularization and other affections [1]. Figure 1(a) shows the original Eye Fundus Image (EFI) and Figure 1(b) shows the corresponding ground truth pixelmap with exudates (hard and soft), microaneurysms and hemorrhages. It also includes the optic disc. The deep learning segmentation network is given a large dataset with images similar to the one shown in Figure 1(a), and pixelmaps similar to Figure 1(b) and learns how to classify each pixel of the image to obtain a pixelmap as close as possible to the pixelmap shown in Figure 1(b). Figure 1(c) is the segmentation output pixelmap, with the lesions and optic disk that were detected by a deep learning network. The semantic segmentations obtained in Figure 1 are classifications of each individual pixel as one of six possible classes that include each type of lesion, plus the background pixels that cover more than 93% of all the area. The learning procedure is based on feeding a training dataset of images and corresponding ground truth pixelmaps to the segmentation network so that it is able to adjust its thousands of inner weights to recognize the lesions. The segmentation network is an evolution of the classification Deep Convolution Neural Network (DCNN). The classification DCNN is a multi-stage neural network with multi-layer convolutional stages having sparse connections, and a multi-layer fullyconnected stage at the end. Each neuron of the convolutional layers calculates from a local region (the receptive field), followed by non-linear activation plus pooling. The segmentation DCNN is a modified DCNN to detect the class of each individual pixel instead of the whole image. In order to do that, the last layers of the classification DCNNs are replaced with a number of up sampling or decoding stages that reconstruct the original size of the image, but outputting a pixelmap where each pixel is an id of the class assigned to the pixel in the original image (e.g. the pixel belongs to lesion X). The DCNN usually learns using a gradient descent algorithm that iteratively adjusts hundreds of thousands of convolutional and neural network weights based in backpropagation of the error (difference between current output and the ground truth at pixel level). Training consists of a large number of iterations adjusting the weights based on the delta error of individual images and corresponding pixelmaps, trying to converge to an accurate estimation of the class of each pixel. Semantic segmentation is evaluated based on testing if the classification of each pixel matches the classification of the same pixel in the ground truth.
Segmentation networks are state-of-the-art in segmentation of medical images, but quality, limitations and comparison of architectures of segmentation networks is still missing in the context of segmentation of lesion in eye-fundus images. After reviewing related work, we build off-the-shelf deep learning architectures and evaluate them on a publicly available dataset, to conclude the strengths and limitations of the approaches and to compare architectures. We investigate the scores on a set of metrics that say the most regarding semantic segmentation, including intersect-over-the-union, precision and recall for each lesion being detected. We also investigate how tuning, data augmentation and patching may or may not improve the results. We conclude that the best segmentation networks outperform related work and include very good scores, such as 87.5% IoU of FCN, but at the same time we show that they have much low scores in other most often overlooked details, such as 17% IoU in microaneurisms due to a large number of false positives. We finalize by discussing the challenges that lie ahead as a consequence of our investigations. This study has a few limitations. First of all, it focuses on the fundamental task of segmentation of lesions using deep learning segmentation networks, but further work is necessary to quantify the influence of segmentation quality in the outcome of further analysis of diabetic retinopathy. Secondly, although the current study already includes thousands of lesions and we used data augmentation techniques to augment the diversity of the dataset, a wider study could be done using thousands of eyefundus images. This work is structured as follows: First we review related work in section 2. Section 3 describes materials and methods, describing the interpretation that metrics should have, then it reviews the structure of alternative off-the-shelf DCNNs for segmentation tasks and finally the experimental setup. In section 4 we show the experimental results, analyze and conclude regarding those results. Finally, section 5 shows conclusions and discusses further work in the future.
Related Works
Given the amazing capabilities of deep learning networks applied to segmentation, researchers were already starting to explore them in segmentation tasks around 2014, where DCNNs were applied to handle, for instance, brain tumour segmentation in the BRATS challenge [2]. Works [3,4] are examples of DCNNs applied around 2014 in that context and reported improved accuracy when compared with the more traditional alternatives based in unsupervised segmentation followed by classification, with continuing focus on the same approaches along the years [5]. The design of the DCNN-based segmentation networks evolved along time. One of the first well-structured network architectures was the Fully Convolutional Network (FCN) [6]. Its approach was to take any DCNN classification network and replace its last layers (the fully-connected network based classifier) by additional convolution layers, followed by a sequence of upsampling layers, increasing the size of the feature maps stepby- step, until the full image size was restored. In FCN the upsampling was based in interpolation, while the convolution layers would adjust their filter coefficients along training epochs based on error back-propagation. The FCN achieved 62% in 2012 PASCAL VOC challenge. An improved design further extended error back-propagation to the deconvolution stages as well, achieving 72.5% on the same challenge. U-Net introduced further innovations [7], such as forwarded cropped feature maps from an encoding layer and a de-coding layer at the same level. Segnet is another deep convolutional encoder-decoder architecture for image segmentation. The architecture of its encoder network is topologically identical to the 13 convolutional layers in the VGG16 network. The decoder network maps the low-resolution encoder feature maps to full pixelwise classification. The novelty of Segnet lies in how pooling max-pooling output indexes are forwarded to the corresponding decoder level, resulting in nonlinear decoding capability. The up-sampled maps are sparse and are then convolved with trainable filters to produce dense feature maps. DeepLab [8] adds new innovations that increase precision when compared to other prior architectures: Atrous Spatial Pyramid Pooling (ASPP) is an approach that segments at different scales simultaneously with different sample rates over convolution feature maps over different actual fields-of-view. This way objects are captured at varied scales. Additionally, probabilistic graphical models are used for improved determination of boundaries of objects. The outputs of the final DCNN layer are combined with a fully connected Conditional Random Field (CRF) to do that, resulting in 79.7% IoU on PASCAL VOC-2012 semantic image segmentation task. Surveys [9-11] review works on automated analsys of Diabetic Retinopathy. Only a few of the works reviewed there have some relation to segmentation of lesions, e.g. Prentasic et al. [12], Gondal at al. [13], Quellec et al. [14], Haloi et al. [15], van Grinsven et al. [16], Orlando et al. [17] and Shan et al. [18]. From those works, [12,15,16,18] do not segment the image and the experimentation in those papers does not evaluate segmentation, instead they classify a small squared window as a type of lesion or not. Evaluation of the approaches uses thousands of windows picked statically based on labels from groundtruths. By contrast, segmentation involves taking the whole image as input and outputting the contours of segments, which requires locating the zones of the lesions and classifying all pixels regarding the segment each belongs to. The remaining works [13,14,17] do include segmentation of the images. [13,14] are based on generating heatmaps from the inner weights of some layer(s) of a convolutional neural network classifying Diabetic Retinopathy. [17] also uses a classification convolution neural network, adding also hand-crafted features that then pass through a random forest classifier of red lesions. Those works report high scores for image-level lesion detection task (near to 100%), which is very different from segmentation. For lesion-level detection, those works report sensitivies for 1 FPI varying between 47 and 50% for hemorrhages, 40 and 57% for hard exudates, 64 to 70% for soft exudates and 7 to 38% for micro-aneurisms. But our focus in this paper is not image-level or lesion-level lesion detection, it is on assessing segmentation networks in detail, focusing on semantic segmentation of lesions. Semantic segmentation is also called scene labeling and refers to the process of assigning a semantic label (e.g. car, people, and road) to each pixel of an image [19]. In semantic segmentation each pixel must be assigned the exact class to which it belongs in reality, and train and test ground truths should be pixelmaps that should identify, as much as possible, the correct class of each pixel. Nevertheless, we include a brief section on results of comparison to those prior works doing lesion detection using the same dataset and evaluation approach used by them, where we conclude that the best segmentation networks outperform those prior approaches.
Materials and Methods
In this section we first review metrics and DCNN architectures that we compare, representing some of the most useful alternatives. Then we define the experimental setup.
Metrics
The assessment of segmentation in general requires metrics that evaluate the degree of overlap of the proposed segments with the actual segments identified in the ground truth masks. It is important to evaluate the degree to which both overlap, and also how close the discovered boundaries match actual boundaries of the segments. The most rigorous way to evaluate the quality of segmentation is based on evaluating the assignment of classes to each and all individual pixel. Most importantly, it is essential to evaluate those for each class (type of lesion and/or structure) instead of only the “global numbers”, since the “global numbers” are heavily influenced by the largest class, the “background”, because it occupies a huge majority of the total number of pixels. A set of metrics is defined next:
Global Accuracy: Global accuracy is the ratio of correctly classified pixels, regardless of class, to the total number of pixels in the image or in all images. Global accuracy provides a single value that is sometimes used to compare approaches. However, it can hide major per-class deficiencies because accuracy of largest classes with most pixels (“background” in EFI images) hides inaccuracies in segmentation of other classes (lesions in EFI);
Class Accuracy: Class accuracy identifies the percentage of correctly identified pixels of each class (each lesion or structure). Class accuracy is the ratio of correctly classified pixels to the total number of pixels in that class, according to the ground truth. In other words, the accuracy score is acc(c)= TPc/(TPc+FNc), where TPc is the number of true positives and FNc is the number of false negatives. Class accuracy conveys relevant information, but it should not be used as a main qualifier of quality of segmentation because it is a partial measure. It reports the quality of the approach regarding segmentation of pixels that belong to the class. Its limitations are easy to understand with as impel example: a DCNN network always returning the same class for all pixel’s scores 100% in this metric for that class.
Mean Accuracy: It is the mean of accuracy over all classes. Being an average, it describes the average behavior, potentially masking deviating behavior of individual classes. Weighted accuracy is a weighted mean, weighted on the number of pixels of each class. The degree of masking is even much larger in weighted accuracy because accuracy of classes with more pixels are better represented in the result.
Intersection over the Union = IoU: IoU is also known as Jaccard coefficient and represents the fraction of pixels of a class classified well to all pixels classified as that class plus pixels of that class classified as another class, IoU = TP/(TP+FP+FN). While accuracy evaluates only against the pixels that actually belong to the class (TP+FN), IoU also considers false positives, which is pixels that are classified as belonging to the class in spite of not belonging to it.
Mean IoU: the mean IoU is the average IoU score of all classes in all images, and weighted IoU is a weighted mean of class IoU, weighted on the number of pixels of each class. Being average metrics, they can potentially mask deficiencies of individual classes.
Boundary contour matching score (BF score): the boundary contour matching score measures the degree to which the actual boundary of regions is matched by predicted boundaries of those regions. A match between boundaries is detected iff the actual and predicted boundary pixel is within a predefined distance (Matlab2018 default 0.75% of the image diagonal). For each class, precision is defined as the ratio of pixel matches of predicted boundary to actual boundary, divided by the number of boundary pixels in the predicted boundary. Similarly, recall is defined as the ratio of pixel matches of actual boundary to predicted boundary, divided by the number of boundary pixels in the actual boundary. The BF score uses the F-measure that is computed from the precision and recall: F=2*P*R/(P+R). As with the previous metrics, there is mean BF-score, weighted BFScore and per class BF-Score, with the same limitations as those described for the previous metrics.
Class precision, recall and confusion matrix: precision measures the fraction of pixels classified as class C that are of class C, and recall measures the fraction of pixels of class C that were classified as class C. The confusion matrix is a square matrix representing the number of pixels of each class (represented in rows) that were classified as each class (represented in columns).
DCNN Segmentation Architectures
DCNN segmentation networks are distinguished by different architectural choices and innovations. We are comparing a set of networks, verifying how the architectural choices reflect in accuracy. Next, we summarize architectural differences between the alternatives, considering our implementations for this work.
Simple: „Simple“ is the most basic encoder-decoder architecture with only 4 layers in each of the two stages- encoding and decoding, plus a softmax and a pixel classification layer for output. The encoding stage has 4 convolution layers, with reluactivation functions, and 4 2x downsampling maxpool layers. The decoding stage has the “opposite”, two de-convolution layers with reluactivation.
encodingLayers = [ conv, relu, maxPoolDownsample2x, conv, relu, maxPoolDownsample2x;]
upsamplingLayers = [ transposedConvUpsample2x, relu, transposedConvUpsample2x, relu]
The convolution layers apply 64 3x3 filters with stride [17], and the deconvolution layers apply 64 4x4 filters.
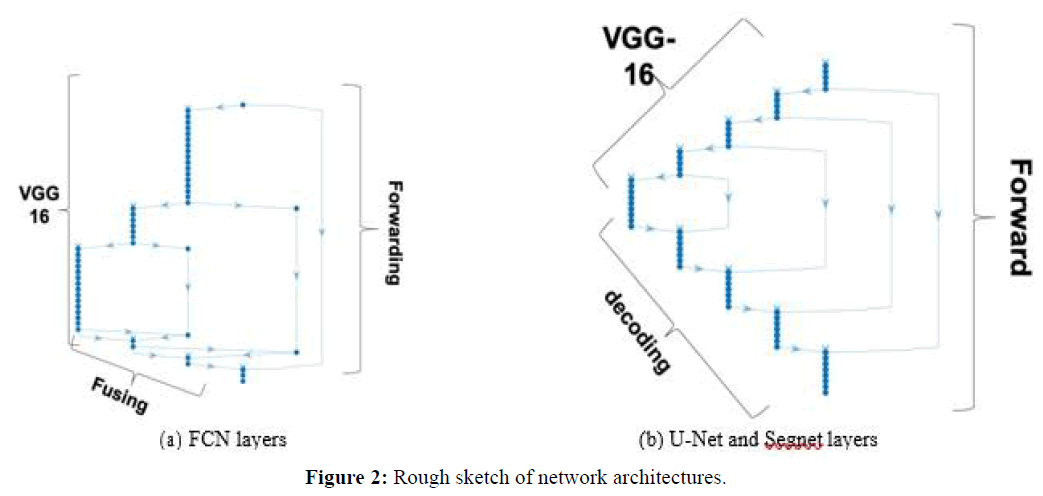
Fully Convolutional Network (FCN): The FCN uses a DCNN classification network (feature extraction or encoding stages), plus a sequence of up-sampling layers (decoding stages) that use interpolation to compute the full image size pixelmap. In FCN backpropagation learning adjusts the weights of the coding layers. Our FCN implementation had 51 layers in total, using VGG-16 as encoding network (VGG-16 has 7 stages corresponding to 41 layers). Figure 2(a) shows a sketch of the architecture, where it is possible to see that most FCN layers are VGG-16, but FCN also forwards feature maps: the pooled output of coding stage 4 is fused with output of the first up-sampling layer that is placed just after stage 7 of VGG16, and the pooled output of coding stage 3 is fused with the output of the second up-sampling layer. Finally, the image input is also fused with the output of the third up-sampling layer, all this followed by the final pixel classification layer. The figure indicates forwarding links and „fusing“ layers.
U-Net and Segnet: Figure 2(b) represents a rough sketch of both the U-Net and Segnet architectures, with VGG-16 as feature extraction (encoding) stages. Contrary to FCN, both these architectures have full decoding stages that deconvolve and are symmetric to the corresponding encoding layers. While U-Net forwards cropped feature maps directly after ReLu regularization at each stage, which are concatenated with the corresponding stage outputs at the destination, Segnet forwards max-pooled outputs and unspools at the destination. This way the decoder upsamples using pooling indices computed in the maxpooling step of the corresponding encoder, to perform non-linear up-sampling. Our U-Net had 5 encoding layers and 70 layers in total, plus connections between the layers. The corresponding Segnet architecture had the same 5 encoding layers and a total of 73 layers.
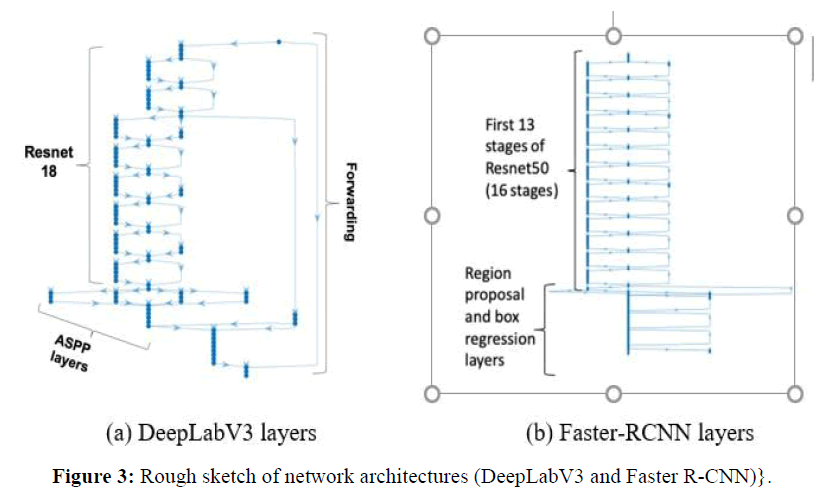
DeepLabV3: DeepLabV3 is the deepest network tested in this work, with 100 layers. Figure 3(a) shows a summary of its main layers. Our DeepLabV3 architecture used Resnet-18 pre-trained network as feature extractor, plus forwarding connections to the the Atrous Spatial Pyramid Pooling (ASPP) layers, indicated in the figure, which enables segmenting of objects at multiple scales. The outputs of the final DCNN layer are combined with a fully connected Conditional Random Field (CRF) for improved localization of object boundaries using mechanisms from probabilistic graphical models. The figure shows that the feature extraction part of our DeepLabV3 implementation is using Resnet-18 layers, with 8 stages and totaling 71 layers, the remaining stages being ASPP plus the final stages.
Faster RCNN: The Faster-RCNN we use is a region-based CNN that uses Resnet-50 as its feature extraction network, to which it adds a region proposal network (RPN) to generate region proposals. The Faster-RCNN also pools CNN features corresponding to each region proposal for object detection. Figure 3(b) shows that the first part of the network is a set of 13 of the 16 stages of Resnet-50 CNN, which has 177 layers, the remaining is the RPN and box classification parts, for a total Faster-RCNN size of 188 layers.
Effects of Patching and Data Augmentation
The original EFI images used in our experiments are quite big (2848x4288). For faster processing and to avoid memory limitations of the GPU, it is convenient to resize those images to smaller sizes, however we were aware that this could have relevant consequences concerning detection of the smallest lesions (e.g. microaneurysm’s and other small instances of lesions). This has motivated us to also compare with the alternative of dividing the original images into patches that would be segmented separately (patching is also a frequent operation in semantic segmentation). The images were divided into four equal-sized slices, simultaneously contributing to augmenting the dataset significantly. The objective was therefore to include evaluation of whether using patching would be beneficial or not.
Experimental Setup
In order to evaluate the architectures and to analyze the quality of segmentation, we needed a set of images together with ground truth pixelmaps classifying each pixel of each image as one of the possible classes. It is quite hard to obtain the ground truth data because it requires experts to label each of the lesions in each of the images comprising the dataset. Luckily this was available in the form of a challenge [20] acquisition of the images being done in an Eye Clinic in Nanded, Maharashtra, India. The IDRID dataset includes 81 EFI images with annotation of individual pixels. the following lesions and structures were annotated: the optic disk, micro-aneurisms, exudates classified as two sub-types, soft and hard, hemorrhages and the „default“ class, background. The equipment used to acquire the images was a Kowa VX-10 alpha digital fundus camera with 50-degree field of view (FOV), centered near the macula. Image resolution was 4288 × 2848, saved as jpg. Experts validated the quality of the images and their clinical relevance. For our work we divided the dataset randomly to obtain 55 training and the remaining testing images (and ground truths). We used a machine running windows 10. The hardware was an intel i5, 3.4 GHz, 16 GB of RAM 1TB SSD disk. A GPU was added to the PC, consisting of an NVIDEA GForce GTX 1070 GPU (the GTX 1070 has a Pascal architecture and 1920 cores, 8 GB GDDR5, with memory speed of 8 Gbps). The network architectures were implemented in Matlab2018 and were pre-tested against an MRI dataset of abdominal organs with known metric outputs to verify that the networks and software were running correctly. This pre-test was positive. For the experiments themselves we defined an SGDM learning algorithm (stochastic gradient descent with momentum 0.9), minibatch with size 16 (decreased if necessary for lack of GPU memory), an initial learning rate of 0.001 and tested the quality of the outputs, adjusting the learning rate whenever the outcome was classifying every pixel as background after converging. Note that we weightbalanced the pixel classification layer to counter the imbalance between classes, with most pixels belonging to the background class. The training would run for 500 epochs, although we would rerun with different settings whenever we noted that there more epochs would be needed for convergence. After pre-tests we found that both U-NET and FCN would easily converge to classifying every pixel as background, in spite of weigh-balancing, which we corrected by decreasing the learning rate to 0.0005 and giving the network architectures more epochs to converge if necessary (we could stop manually when we noted visually convergence was already visible for many epochs). DeepLabV3 needed no such modifications, since it would converge nicely to a better classification of lesions and all classes with the initial learning rate of 0.001. Our reported results were preceded also by extensive tests with many other alternatives that proved sub-optimal when compared with our final results, therefore we do not report on them. One such direction was adding data augmentation, which would artificially increase significantly the number of images by inserting random changes in the existing images. We tested with random rotations and translations. Another direction of testing prior to final experiments was testing several image resizing options.
Experimental Results
Timings
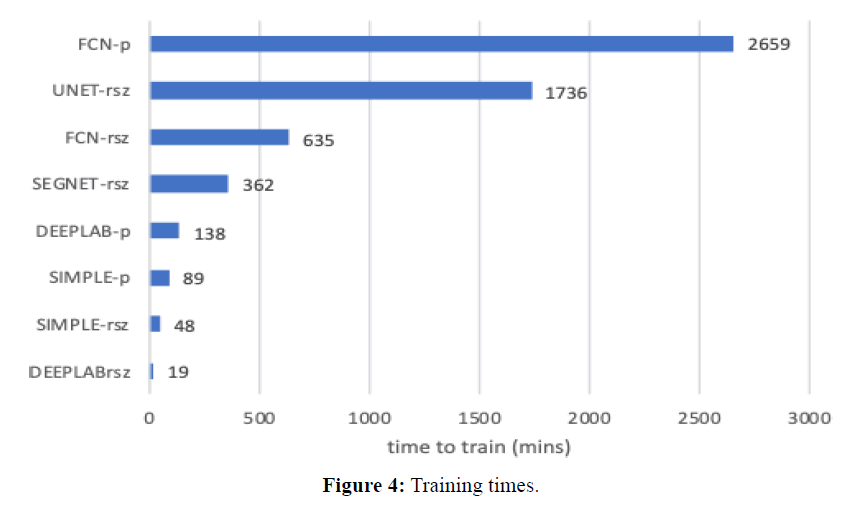
Training times are shown in Figure 4 in units of minutes. Training of images with sizes 1024x2048 is denoted as (-rsz), while training of patches is denoted as (-p). Note that patches take much longer, since the datasets are much larger (4 patches per image). UNET was slowest (1736 mins), then FCN was slowest (635 mins rsz, 2659 mins patches). DeepLabv3 is much faster comparatively (19 mins resized; 138 mins patched). In what concerns segmenting new images, a quick experiment with 10 images resulted in the following: FCN, 1024 × 2048 rsz, per image mean= 13.35 secs, std= 0.84 secs; DeepLabv3, 1024x2048 rsz, per image mean = 5.90 secs, std = 0.69 secs.
Visualization of Test Images and Outputs
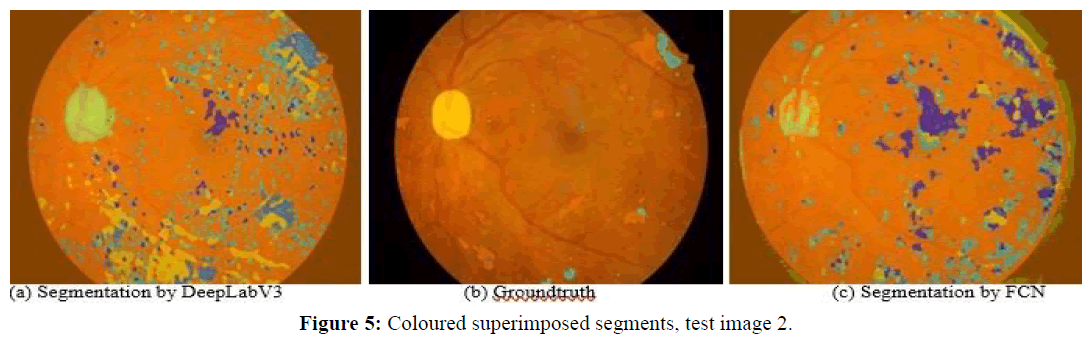
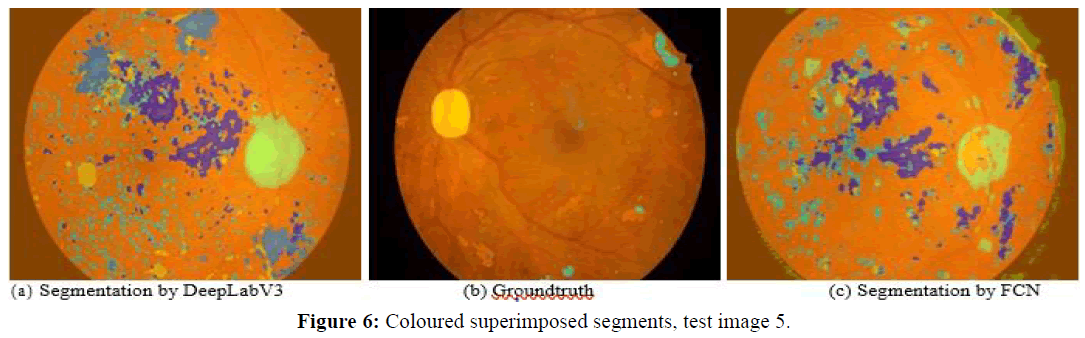
Next, we observe four images and the corresponding segmentations given by the two best performing approaches (DeepLabV3 and FCN). Figures 5 and 6 show test images 2 and 5 with coloured superimposed segments, while Figures 7 and 8 show images 67 and 70 with colored pixelmaps in separate. From Figures 5 and 6 we conclude: (1) FCN has some deficiencies segmenting the optical disk (parts of the optical disk areas uncovered), while DeepLabV3 is much better, but still not perfect (spills over to the background). In what concerns lesions, both have a lot of false positive “noise” (regions incorrectly marked as lesions in the background), perhaps less in the case of FCN, and FCN also has some “hallo noise” marked as lesions in the boundary of the eye fundus images.
Figures 7 and 8 use a different perspective for two other images, with pixelmaps separated from the images. Analyzing the pixelmaps, we can see that the ground truth pixelmaps (a) have significantly fewer lesion regions than the number of regions marked as lesions in the segmentations of either DeepLabV3 (c) or FCN (d), DeepLabV3 being much worse (more pixel regions falsely classified as lesion) in that respect. Still, the optic disk was well segmented for these images in both networks, and both approaches were able to detect most lesions, the main problem being large amounts of false positive noise in the form of background regions marked as lesions (worse in DeepLabV3 than in FCN).
Experimental Results
Our experimental results are presented in this section and analyzed in the next one. „Global“ accuracy of the various approaches is shown in Table 1 (including also the RCNN alternative). These initial global results are further detailed by analysis of accuracy of each class (each lesion, plus the optic disk) in Tables 2, 3 and 4, where we report both accuracies, intersectover- the-union and the boundary score. Finally, we also report the confusion matrixes returned by the segmentation toolbox. Tables 5 and 6 are confusion matrices for DeepLabV3 and for FCN respectively, given as absolute values over all pixels of all images, which we then used to calculate per-class precision and recall that are shown in Tables 7 and 8. Since we also wanted to understand how patching affected accuracy, we include Table 9, which compares to no-patching but resizing instead. Finally, we show a significant improvement in DeepLabV3 results by applying a different loss function than the default (cross entropy) in both Table 10 and 11. The applied loss function was mean IoU. We decided to try mean IoU to try to optimize IoU.
| Method | Global Accuracy | Mean Accuracy | Weighted IoU | Mean IoU | MeanBFScore |
| FCN | 89.50 | 74.60 | 87.50 | 37.90 | 48.50 |
| DeepLab | 81.20 | 84.10 | 78.50 | 32.80 | 33.60 |
| U-Net | 58.70 | 59.80 | 56.20 | 16.10 | 19.60 |
| Segnet | 52.70 | 45.40 | 50.20 | 14.20 | 17.50 |
| Simple | 49.00 | 54.60 | 46.40 | 11.60 | 19.10 |
| Faster-RCNN | - | - | - | 29.6 | - |
Table 1: Accuracy of 1K x 2K images.
| Class | FCN | DeepL | U- NET | Segnet | Simple | F- RCNN |
| Background | 89.9 | 80.9 | 58.4 | 52.3 | 48.3 | - |
| OpticDisc | 95.3 | 96.3 | 94.0 | 90.5 | 93.9 | 91.3 |
| SoftExudates | 61.0 | 83.1 | 47.9 | 24.8 | 29.5 | 11.7 |
| Hemorrhages | 58.0 | 64.3 | 35.6 | 47.8 | 28.3 | 5.4 |
| HardExudates | 80.4 | 96.2 | 55.7 | 36.6 | 64.8 | 22.1 |
| Microaneurs | 63.0 | 83.9 | 67.5 | 20.2 | 62.9 | 8.8 |
Table 2: Accuracy of each class using 1K x 2K images.
| Class | FCN | DeepL | U- NET | Segnet | Simple |
| Background | 89.5 | 80.6 | 58.1 | 51.9 | 48.1 |
| OpticDisc | 76.8 | 68.0 | 17.3 | 16.0 | 10.1 |
| SoftExudates | 21.4 | 14.0 | 1.3 | 0.9 | 0.5 |
| Hemorrhages | 21.1 | 14.3 | 2.5 | 1.9 | 3.1 |
| HardExudates | 16.9 | 19.1 | 16.6 | 13.9 | 6.8 |
| Microaneurs | 1.7 | 1.0 | 0.6 | 0.3 | 0.7 |
Table 3: IoU of each class, 1K x 2K.
| Class | FCN | DeepL | U-NET | Segnet | Simple |
| OpticDisc | 70.5 | 54.1 | 18.9 | 5.0 | 21.0 |
| Background | 59.9 | 43.9 | 35.6 | 31.1 | 36.9 |
| HardExudates | 54.5 | 46.2 | 30.7 | 41.4 | 24.3 |
| SoftExudates | 47.9 | 26.6 | 5.3 | 3.4 | 4.7 |
| Hemorrhages | 37.6 | 20.1 | 11.9 | 9.5 | 12.7 |
| Microaneurysms | 20.9 | 9.5 | 7.1 | 7.8 | 6.8 |
Table 4: BF-Score, 1K x 2K.
| Class | Bground | MAneu | Haemo | HardEx | SoftEx | OpticD |
| Bground | 5667700 | 494540 | 341120 | 371090 | 70506 | 42823 |
| MAneu | 292 | 4737 | 573 | 104 | 2 | 0 |
| Haemo | 22217 | 11517 | 67289 | 1424 | 1292 | 245 |
| HardEx | 1204 | 579 | 34 | 84552 | 507 | 15 |
| SoftEx | 2036 | 652 | 654 | 2550 | 14588 | 263 |
| OpticD | 3061 | 127 | 39 | 507 | 260 | 130950 |
Table 5: Confusion Matrix (absolute), DeepLab V3.
| Class | Precision | Recall |
| Background | 0.99 | 0.81 |
| Microaneurysms | 0.01 | 0.83 |
| Hemorrhages | 0.16 | 0.65 |
| HardExudates | 0.18 | 0.97 |
| SoftExudates | 0.17 | 0.70 |
| OpticDisc | 0.75 | 0.97 |
Table 6: Precision and Recall, DeepLab V3.
| Class | Bground | MAneu | Haemo | HardEx | SoftEx | OpticD |
| Background | 12195251 | 473173 | 248019 | 563172 | 36800 | 52395 |
| Microaneurysms | 2238 | 8527 | 2400 | 334 | 24 | 22 |
| Hemorrhages | 40184 | 15049 | 87294 | 6486 | 916 | 558 |
| HardExudates | 5164 | 1425 | 9554 | 122508 | 9369 | 4318 |
| SoftExudates | 3824 | 668 | 1050 | 2626 | 15614 | 1810 |
| OpticDisc | 8147 | 276 | 1530 | 1150 | 385 | 233 516 |
Table 7: Confusion Matrix (absolute), FCN.
| Class | Precision | Recall |
| Background | 1.00 | 0.90 |
| Microaneurysms | 0.02 | 0.63 |
| Hemorrhages | 0.25 | 0.58 |
| HardExudates | 0.18 | 0.80 |
| SoftExudates | 0.25 | 0.61 |
| OpticDisc | 0.80 | 0.95 |
Table 8: Precision/Recall Matrix. FCN.
| Method | MeanAcc | GlobalAcc | MeanIoU | Weighted.IoU | MeanBFScore |
| DeepLab | 84.1 | 81.2 | 32.8 | 78.5 | 33.6 |
| FCN | 74.6 | 89.5 | 37.9 | 87.5 | 48.5 |
| FCN-patch | 72.3 | 93.5 | 39.0 | 91.1 | 53.1 |
| DeepLab- patch | 70.0 | 75.9 | 24.0 | 72.7 | 43.8 |
| Simple-patch | 61.7 | 61.7 | 16.4 | 59.0 | 23.3 |
| Simple | 54.6 | 49.0 | 11.6 | 46.4 | 19.1 |
Table 9: Comparing Patching of 2x larger EFI image VS no patching?
| Class | IoU modified loss | IoU default loss |
| Backgnd | 97 | 89 |
| Maneurysms | 17 | 1.70 |
| Hemorrhages | 22 | 21 |
| HardExudates | 55 | 17 |
| SoftExudates | 45 | 21 |
| OpticDisc | 75 | 77 |
Table 10: Per class IoU on DeepLabV3: default (crossEntropy) loss vs modified loss.
| Loss | Global Accuracy | Mean Accuracy | Mean IoU | Weighted IoU | Mean BFScore |
|---|---|---|---|---|---|
| modified loss | 97 | 61 | 52 | 95 | 58 |
| default loss | 90 | 75 | 33 | 88 | 35 |
Table 11: Global metrics on DeepLabV3: Comparing results, default (crossEntropy) loss vs modified loss.
Discussions
The discussion is organized by parts, each first indicating which tables or figures are discussed and then explaining and reaching conclusions regarding those tables or figures.
Analysis of Table 1, global metrics: The best accuracy in the table was achieved by FCN (~90%), and DeepLab accuracy was also relatively high (~81%). The remaining network architectures tested exhibit low accuracies, between 40 and 59%. If we compare with Simple, accuracy of FCN improves from 49% (Simple) to 90% (FCN), but on the other hand Segnet improved only 4% and U-net 6% to Simple. The mean accuracy and weighted IoU in the same table confirm these results (note however that mean accuracy of FCN decreases significantly (while that of DeepLab increases from 81% to 84%). The two last columns of the same table reveal a problem with the previously analyzed metrics: using mean IoU and mean BF-Score this time we can see that the values are very low for every network architecture (e.g. 11% to 40% mean IoU), including the ones previously classified as best. This is not an error; it is because the previous metrics were masking deficiencies significantly. The reason for the discrepancy is that the background pixels occupy more than 95% of all pixels, and the optic disk is also around two percent of all pixels). These two classes are much easier to segment than lesions because they have fairly constant properties (e.g. most of the quadrature of the Eye Fundus is always background, standing in the same positions in all images; the optic disk has a common shape (round) and size, with similar color properties in most EFI images as well). That means any metric that weights over all pixels or classes will represent mostly the quality of segmentation of the background and the optic disk, not the lesions. This also hints that the lesions are not well segmented using any of the architectures.
Comparison with Faster R-CNN: For the Faster-RCNN we only report mean IoU (29.6%), lower than FCN (38%) and DeepLab (33%), but much better than the remaining architectures. Note that in the case of R-CNNs quality is measured by comparing the minimum-bounding rectangles (MBR) output by the architecture to the MBR of the ground truth.
Analysis of table 2, per-class accuracy: Observation of accuracy of each individual type of structure reveals very interesting details: first of all, we focus only in FCN and DeepLab because the remaining architectures have much worse results in this table. We can see that the optic disk has high accuracy (around 95%), and the background is also reasonably wellsegmented (FCN: 90%, DeepLab: 81%). From the remaining lesions, hard exudates also exhibit high accuracy (FCN: 80%, DeepLab: 96%), the other lesions had values between 58% and 83% depending on which of the two networks and the lesion. The conclusion is that, according to this metric, optic disk, background and hard exudates are well segmented (85 to 96% accuracy), the remaining lesions are lower, in the range of (60% to 84%). However, accuracy hides deficiencies that IoU reveals better, as we discuss next.
Why does IoU reveal deficiencies and accuracy mask those deficiencies in EFI segmentation? The formula of mean accuracy is the True Positives divided by the sum of True Positives with False Negatives, while IoU adds also False Positives in the denominator. the DCNNs were very good identifying lesion pixels as lesions, but confound many background pixels for lesions. Since those are False Positive when we are calculating accuracy of lesions, they are not reflected in the result reported by accuracy, but are reflected in IoU of those lesions, since IoU adds False Positives to the denominator.
Analysis of Tables 3 and 4: These tables report measurements of two important metrics: Intersect-over-the-union (IoU) and the boundary F-score (BFScore). Once again, we focus only on the architectures with best results (FCN, DeepLab), since the other ones have very low scores comparatively. According to IoU results, all lesions have low scores, between 1.7% and 22% in the case of FCN and between 1% and 14% for DeepLab. The optic disk has higher IoU scores (FCN:77%, DeepLab:68%). This IoU metric is revealing the most relevant deficiency in the segmentation outcomes. From FCN and DeepLab values for class accuracies in Table 2 we can see that lesion pixels are still reasonably well identified as belonging to that lesion (58% to 96% accuracies), depending on lesion and architecture. But from the much lower values of IoU in Table 3 (1% to 21%) we conclude that large background areas that are not lesions are also identified as lesions (False Positive lesions). This is also apparent in the visualizations seen in a previous subsection. The addition of False Positives in the denominator of the formula of IoU allows this metric to reveal this deficiency much better. The conclusion is that FCN and DeepLab were able to identify lesions reasonably well but at the expense of also classifying many neighboring background pixels as lesions. There is a need to improve the approaches to avoid this limitation, e.g. by filtering false positives better. Note also that BF-Scores of individual lesions were higher than IoU of those classes, which is probably related to the threshold used in BF-Score to measure the distance from segmentation boundaries to ground truth boundaries.
Analysis of Tables 6 and 8: Tables 6 and 8 (obtained from confusion matrices of Tables 5 and 7, show the per-class precision and recall of DeepLabV3 and FCN, respectively. The recall values shown are high and coincide with the values of per-class accuracy shown before in Table 2, confirming that per-class accuracy reported by Matlab is the same as per-class recall (TP/(TP+FN)), the fraction of all pixels of one class that were correctly classified as that class. Precision, on the other hand, is much lower for most classes and very low for some lesions (e.g. in DeepLabV3 we had microaneurisms:1%, hemorrhages 16%, hard exudates 18%, soft exudates 17%). It means that a significant fraction of all pixels classified as a specific lesion are false positives, most frequently background pixels. (note also the detail that the only cases with a slightly lower recall (65%, 70%) are hemorrhages and soft exudates. These slight decreases are due to some confusions between the pairs Microaneurysms-hemorrhages and soft-hard exudates, because they have some similar characteristics, such as color).
Analysis of Table 9: Our experimentations with patching, shown in Table 9, were also interesting. Since the images were very big, we had to reduce their sizes from 2048x4096 to 1024x2048 in most experiments. The objective of using patching in this context was to evaluate whether it would be better to keep the full image sizes and apply a kind of patching (dividing the images into quadrants) to avoid reducing the image size and this way avoid difficulties detecting the smallest lesions, versus the normal procedure we adopted. But Table 9 shows that the various accuracy metrics used did not improve significantly by using patching.
Analysis of Tables 10 and 11: The results we achieved by modifying the training loss function involved a significant improvement of quality of segmentation of lesions (in particular, IoU of microaneurysm’s improved from 1.7% to 17%, hard exudates from 17% to 55% and soft exudates from 21% to 45%). This confirms the fact that metric interpretation and use is crucial to correctly assess and improve the approaches, and also signals that more work on loss functions and training details is crucial in the future.
Brief on Comparison to Prior Work
Our focus in this work was detailed analysis of semantic segmentation results, but we also started work independently to compare with prior works using dataset [21] and the same approach those works use to evaluate quality of lesion detection. We measured sensitivity on 10 FPI of DeepLabV3. The results were: 87% for hemorrhages, 97% for hard exudates, 92% for soft exudates and 52% for micro-aneurisms. This compares with the following results of [14], one of the tops performing prior works: 71% for hemorrhages, 80% for hard exudates, 90% for soft exudates and 61% for micro-aneurisms. The conclusion is that, apart from micro-aneurisms, DeepLabV3 was superior when compared with prior work. F.
Conclusions from Experimental Work
Some important conclusions standout from the previous analysis of the results:
a) how successful is it to segment most difficult, small and hard to identify lesions, and how successful is it to segment larger and easier to identify objects such as the optic disk? Segmenting lesions is not very successful (e.g. IoU of 2% microaneurysm’s, 17% to 21% other lesions on FCN), segmenting larger objects such as the optic disk is much more successful;
b) is there hope that the segmentation quality using deep learning can be improved in the future, how? Yes, the fact that accuracy is very high means that most deficiencies are associated with background being classified as lesion (false positives), we have to improve approaches to add filters that will filter out those false positives;
c) in the light of the results, why can some metrics fool us and how should they be interpreted and used to avoid mistaken conclusions, how should we interpret the differences in metrics? We have explained why accuracy and metrics over all pixels were reporting high values that were very different from IoU or BFScore, and we have explained why investigating IoU of individual lesions is very important. Metrics must be correctly interpreted, but all the studied metrics are still useful for their meaning, e.g. high accuracy means pixels that are lesions are very well identified as such;
d) the comparison of the approaches, concluding which is best and how much they improve compared to the reference elementary architecture. When comparing with Simple (the reference architecture), we conclude that all the other architectures were able to achieve much better quality (e.g. global accuracy Simple: 49%, FCN:89.5%, mean IoU Simple:11.6%, FCN:37.9%), and the two architectures that were able to achieve best performance were DeepLabv3 and FCN.
e) since many lesions are small or very small, is there an advantage in enlarging the images and doing the segmentation on patches of those enlarged images? is a Faster-RCNN approach based in MBRs better? The results have shown that it was not very useful to apply patching on the larger images, since there was not a very relevant improvement, even for the smallest lesions. Note that this could be related to the fact that patches are less uniform than whole EFI images, since they are from different parts of the EFI image, in some occasions actually cropping structures such as the optic disk. This may make it more difficult to be accurate, as we noted in the form of more accuracy oscillations during the training process. Using the region-proposals based method we achieved 29.6% mean accuracy, far lower than either FCN or DeepLabV3 accuracies.
f) as we have investigated in this work, metrics assume a huge importance for the quality of segmentation. We therefore suspected that careful use of metrics in the loss function of the crucial network training phase would have important consequence, and we have shown a dramatic improvement of the results for some of the worst segmented lesions by replacing the default training loss function by one that better reflects the degree of match between regions of classes (Tversky index). More work on loss functions and training details is crucial in the future.
Conclusions and Future work
In this experimental work we have built a set of state-of-the-art segmentation DCNN architectures to evaluate the quality of those architectures segmenting EFI images for Diabetic Retinopathy lesions. If those are capable of good results, then the approaches can be used off-the-shelf. We focused on the metrics and their correct interpretation in order to explain where and why the approaches fail. We highlighted that it is easy to misinterpret the results returned by metrics, since some metrics, although also conveying useful information, hid deficiencies. Then we have shown that all tested architectures have difficulty achieving high IoU, and explained the discrepancy between IoU and accuracy. The analysis of results revealed that the best approaches were acceptable (not very good) at identifying lesions as such, but at the expense of also labeling many background pixels as lesions, and in some cases also confounding between different lesions. Larger and more constant structures (background and optic disk) were better segmented, but accurate segmentation of the smaller and more variable lesions need improvements. Since metrics are so relevant for the assessment, we also hypothesized that they might have an important impact during the network training phase. Accordingly, by changing the training loss function we were able to dramatically improve the IoU of the worst segmented lesions. Future work should focus on improving the quality of segmentation of individual lesions, with further work on training loss functions, other architectural details of networks and possibly filtering out false positive lesions that are part of the background using some postprocessing.
Acknowledgments
We use the IDRID challenge dataset for this work [20] We would like therefore to thank the IDRID challenge organizers for sharing the dataset.
Conflict of Interest
The authors declare that they have no conflicts of interest.
REFERENCES
- Wilkinson C, Ferris III FL, Klein RE, Lee PP, Agardh CD, Davis M, et al. Proposed international clinical diabetic retinopathy and diabetic macular oedema disease severity scales. Ophthalmology. 2003; 110(9):1677-1682.
- Menze B, Reyes M, Farahani K, Kalpathy-Cramer J. Brain tumour segmentation challenge, MICCAI-BRATS. 2014.
- Urban G, Bendszus M, Hamprecht F, Kleesiek J. Multi-modal brain tumor segmentation using deep convolutional neural networks. Proceedings of Multimodal Brain Tumour Segmentation Challenge 2014.
- Zikic D, Brown M, Ioannou Y, Criminisi A. Segmentation of brain tumor tissues with convolutional neural networks. Proceedings of Multimodal Brain Tumour Segmentation Challenge 2014.
- Havaei M, Davy A, Warde-Farley D, Biard A, Courville A, Bengio Y, et al. Brain tumour segmentation with deep neural networks. Medical Image Analysis. 2017; 35: 18-31.
- Long J, Shelhamer E, Darrell T. Fully convolutional networks for semantic segmentation. Proceedings of the IEEE conference on computer vision and pattern recognition. 2015; 3431-3440.
- Ronneberger O, Fischer P, Brox T. U-net: Convolutional networks for biomedical image segmentation. In International Conference on Medical image computing and computer-assisted intervention. MICCAI 2015. Springer, Cham. 2015; 234-241
- Chen LC, Papandreou G, Kokkinos I, Murphy K, Yuille AL. Deeplab: Semantic image segmentation with deep convolutional nets, atrous convolution, and fully connected CRFs. IEEE transactions on pattern analysis and machine intelligence. 2017; 40(4): 834-848.
- Qureshi I, Ma J, Abbas Q. Recent development on detection methods for the diagnosis of diabetic retinopathy. Symmetry. 2019; 11(6): 749.
- Asiri N, Hussain M, Al Adel F, Alzaidi N. Deep learning-based computer-aided diagnosis systems for diabetic retinopathy: A survey. Artificial intelligence in medicine. 2019; 99:101701.
- Raman R, Srinivasan S, Virmani S, Sivaprasad S, Rao C, Rajalakshmi R. Fundus photograph-based deep learning algorithms in detecting diabetic retinopathy. Eye. 2019; 33(1): 97-109.
- Prentašić P, Lončarić S. Detection of exudates in fundus photographs using convolutional neural networks. In 2015 9th International Symposium on Image and Signal Processing and Analysis (ISPA). 2015; 188-192.
- Gondal WM, Köhler JM, Grzeszick R, Fink GA, Hirsch M. Weakly-supervised localization of diabetic retinopathy lesions in retinal fundus images. In 2017 IEEE international conference on image processing (ICIP). 2017; 2069-2073.
- Quellec G, Charrière K, Boudi Y, Cochener B, Lamard M. Deep image mining for diabetic retinopathy screening. Medical image analysis. 2017; 39: 178-193.
- Haloi M. Improved microaneurysm detection using deep neural networks. arXiv. 2015; 1505: 04424.
- Van Grinsven MJ, van Ginneken B, Hoyng CB, Theelen T, Sánchez CI. Fast convolutional neural network training using selective data sampling: Application to hemorrhage detection in color fundus images. IEEE Transactions on Medical Imaging. 2016; 35(5): 1273-1284.
- Orlando JI, Prokofyeva E, del Fresno M, Blaschko MB. An ensemble deep learning-based approach for red lesion detection in fundus images. Computer Methods Programs Biomed. 2018; 153: 115-127.
- Shan J, Li L. A deep learning method for microaneurysm detection in fundus images. In 2016 IEEE First International Conference on Connected Health: Applications, Systems and Engineering Technologies (CHASE) 2016; 357-358.
- Yu H, Yang Z, Tan L, Wang Y, Sun W, Sun M, Tang Y. Methods and datasets on semantic segmentation: A review. Neurocomputing. 2018; 304: 82-103.
- Porwal P, Pachade S, Kamble R, Kokare M, Deshmukh G, SahasrabuddheV, et al. Indian diabetic retinopathy image dataset (idrid). IEEE Dataport. 2019.
- Kauppi T, Kalesnykiene V, Kamarainen JK, Lensu L, Sorri I, Raninen A, et al. The DIARETDB1 diabetic retinopathy database and evaluation protocol. In: Proc BMVC. Warwik, UK. 2007.